Geometria Graceli e cálculo relativo diferencial [/tempo] em
relação ao movimento de das coordenadas.
Coordenadas móveis variáveis Graceli.
Autor : Ancelmo Luiz Graceli.
Imagine uma bola lançada de um ponto a outro de um campo e este
campo em movimento rotacional, logo, em relação a cada ponto em relação ao
tempo, e ao movimento rotacional do campo temos pontos tangenciais, formando
uma curva diferencial em relação a cada segundo do tempo. e
vb + r/t [ sentido de rotação do campo que se afasta do sentido de
velocidade da bola].
vb – r /t [sentido de rotação do campo que se do sentido de
velocidade da bola].
]
Em relação a uma bola lançada no alto temos uma forma diferencial
em relação ao movimento da base [campo] e esta forma varia em relação a subida
e descida da bola.
Vb + r/t + s
Vb + r/t – s
Vb - r/t + s
Vb - r/t – s
E com o campo que se move na forma de ondas com uma bola lançada
sobre ondas temos outra forma ondulatória diferencial
Em com uma bola lançada ao alto sobre o mar temos uma diferenciação
em relação as ondas, e a subida e descida da bola.
Em com uma base de um campo com curvas com declives e subidas e em
rotação, e com a bola subindo e descendo temos uma variabilidade em relação a
estes quatro elementos fundamentais.
Vb + r/t +osc ondas+ s
Vb + r/t + osc ondas– s
Vb - r/t +osc ondas+ s
Vb - r/t+ osc ondas – s
Geometria Graceli e cálculo relativo diferencial [/tempo] em
relação ao movimento de das coordenadas.
Coordenadas móveis variáveis Graceli.
Autor : Ancelmo Luiz Graceli.
Imagine uma bola lançada de um ponto a outro de um campo e este
campo em movimento rotacional, logo, em relação a cada ponto em relação ao
tempo, e ao movimento rotacional do campo temos pontos tangenciais, formando
uma curva diferencial em relação a cada segundo do tempo. e
vb + r/t [ sentido de rotação do campo que se afasta do sentido de
velocidade da bola].
vb – r /t [sentido de rotação do campo que se do sentido de
velocidade da bola].
]
Em relação a uma bola lançada no alto temos uma forma diferencial
em relação ao movimento da base [campo] e esta forma varia em relação a subida
e descida da bola.
Vb + r/t + s
Vb + r/t – s
Vb - r/t + s
Vb - r/t – s
E com o campo que se move na forma de ondas com uma bola lançada
sobre ondas temos outra forma ondulatória diferencial
Em com uma bola lançada ao alto sobre o mar temos uma diferenciação
em relação as ondas, e a subida e descida da bola.
Em com uma base de um campo com curvas com declives e subidas e em
rotação, e com a bola subindo e descendo temos uma variabilidade em relação a
estes quatro elementos fundamentais.
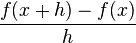
+ r/t +osc ondas+ s
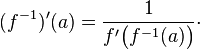+ r/t + osc ondas– s
- r/t +osc ondas+ s
- r/t+ osc ondas – s
.
postado por mathematician, physicist and philosopher Ancelmo Luiz Graceli @ 06:29
0 Comentários
0 Comentários:
Postar um comentário
Assinar Postar comentários [Atom]
<< Página inicial